1. 三种时距曲线方程与实际走时的误差分析
研究对比在不同排列长度情况下,分别用双曲线、含高次项的地震波走时曲线方程以及含各向异性参数的地震波走时曲线方程共三种方法分析计算层状介质反射波走时与真实地震波走时的误差,并以该分析结果为依据,选择误差最小的、最合适的反射波时距曲线方程进行速度分析,得到更加准确的地层速度信息。模型共四层,如图1所示。
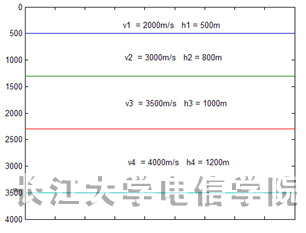
图1 均匀层状介质模型
图2是模型I埋深3500m的第四层反射界面走时误差图。排列长度与目的层埋深之比 时,情况与上两层基本相同,当 时,可以从图2(b)以及表看到含高次项方法的非双曲线方法计算走时的相对误差超过6%,而双曲线方法计算走时的相对误差尚不到6%,说明含高次项方法的非双曲线方法在这种情况下不能很好地描述地震波的走时特点。但是从图2(b)以及表仍然可以看到随着排列长度的增加,含各向异性参数方法计算的反射波时距曲线与理论时距曲线之间的偏差仍然是最小的。

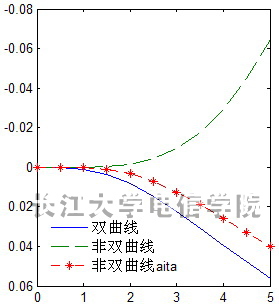
(a) 反射波走时曲线 (b) 走时误差
图2 第四层的走时误差分析
表2 模型I三种方法计算反射波走时与实际走时误差(%)
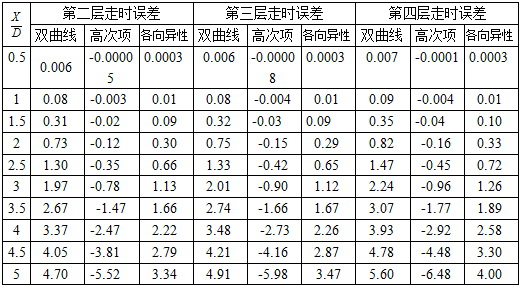
针对模型的三个目的层,利用三种方法计算反射波走时与理论走时的相对误差见表2。从数据结果可以看到,排列长度与目的层埋深 时,三种方法的相对误差都在0.01%以下,因此在短排列的情况下就可以选择比较简单的常规速度分析方法进行速度分析;当排列长度与目的层埋深 时,常规双曲线方法的相对误差最大,含高次项方法计算的相对误差最小;当排列长度与目的层埋深 时,含高次项方法计算的相对误差最大,超过了双曲线的方法,但含各向异性参数方法计算的相对误差最小。因此对于长排列的地震数据,含各向异性参数方法在描述实际地震波走时方面是最精确的。
2. 用非双曲线时距曲线方程进行速度分析
假设最大炮检距与第五层目的层埋深之比 ,分别用常规双曲线方法和非双曲线的方法进行速度分析,其准则函数曲线如图9所示。分析图9(a)显示的常规双曲线准则函数曲线,曲线峰值所显示的各层能量峰值逐渐减小,而这种减少对速度的正确提取是非常不利的。而图9(b)所示的非双曲线速度扫描的准则函数曲线,各层对应的准则函数曲线峰值接近。说明这种非双曲线描述很好地反应了地震波走时特点,更接近实际地震波的反射波时距曲线。

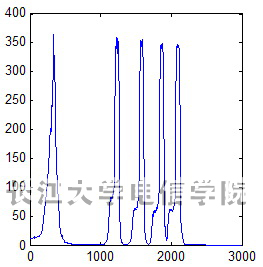
(a)双曲线速度分析 (b)非双曲线速度分析
图9 两种速度分析准则函数对比(X/D=2)
表3 两种分析方法计算的层速度比较(X/D=2)
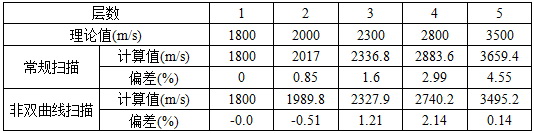
表3显示了用常规速度分析和非双曲线速度分析方法得到的层速度值。非双曲线方法分析得到的第五层层速度值非常接近模型的层速度,相对于用双曲线方法计算的结果有很大地提高。
分别利用常规速度扫描得到的叠加速度进行正常时差校正和利用非双曲线方法计算得到的短排列时差速度进行各向异性的时差校正。动校正后CMP道集结果见图10。通过对比可以看到,对于长排列的地震数据,常规速度分析不能将同相轴准确校平,从而不能得到准确的叠加效果,进而影响偏移效果。而非双曲线速度分析方法能够把同相轴基本校平,这对于后续处理是非常有意义的。
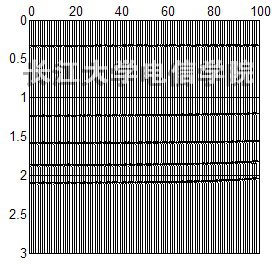
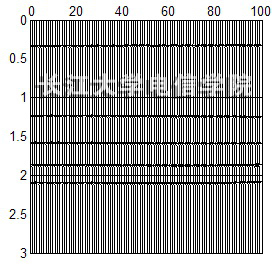
(a)常规速度分析动校正结果 (b) 非双曲线分析动校正结果
图10 动校正结果对比( X/D=2)
3. 非双曲线的速度分析在实际资料中的应用
在非双曲线速度分析的基础上,进行各向异性动校正,得到的叠加剖面如图11(b)所示。对比图11(a),可以看到在图中所示矩形框内,叠加剖面的能量和连续性得到了加强,叠加剖面质量得到了一定的改善。

(a) 常规速度扫描方法

(b) 双参数速度扫描法
图11 两种速度扫描方法处理得到的叠加剖面
项目支撑
1. 地震勘探野外监控和评价系统,石油天然气集团公司,2003
2. 非地表一致性静校正方法研究,高等学校博士学科点专项科研基金项目,2004
3. VSP与地面地震联合处理和解释研究项目中石油东方物探,2007
4. 徐深21-1井区3D-VSP和全方位三维地面地震采集、处理及解释,大庆石油管理局,2007
5. 大庆徐家围子井地联合勘探技术现场试验,大庆石油管理局,2008,
6. 非双曲线的地震波走时研究,长江大学,2009
7. 基于井地联采数据的各项异性研究,中石油东方物探,2009
8. 大型油气田及煤层气开发——复杂油藏地球物理配套技术,2009
9. 南马庄潜山深层低信噪比区精细速度模型的建立非法研究,中石油东方物探,2010
10. 零井源距VSP数据处理和井驱参数求取研究,中石油东方物探,2012
11. 古潜山三维地震观测方向对成像速度的影响分析中石油东方物探,2013